Question

Ross and Chandler are carrying a 150 kg crate up a flight of stairs. The crate is 2.0 m long and 1.5 m high, and its center of gravity is at its center. The stairs make a 45.0° angle with respect to the floor. The crate also is carried at an 45.0° angle, so that its bottom side is parallel to the slope of the stairs. If the force each person applies is vertical, what is the magnitude of each of these forces

Answer 1

The magnitude of each force is 1309 N and 105 N

Step-by-step explanation:

The reaction at each lifter due weight and overturning effect (R₁, R₂) is given as:

`R_1=(150)/(2) cos(45^0) +(1.5)/(2+1.5) *150sin(45^0)=53.03 +45.46=98.49kg\\R_2=(150)/(2) cos(45^0) -(1.5)/(2+1.5) *150sin(45^0)=53.03-45.46=7.57kg`

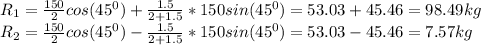
g = 9.8 m/s²

`R_1=98.49*g=98.49*9.8=925.904N\\R_2=7.57*g=7.57*9.8=74.186N`

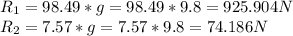
Resolving the reactions to the vertical direction, we get:

`R_(1v)=(R_1)/(cos(45^0)) =(925.904)/(cos(45^0))=1309N\\ R_(2v)=(R_2)/(cos(45^0)) =(74.186)/(cos(45^0))=105N\\`

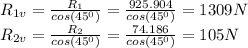
The magnitude of each force is 1309 N and 105 N