Answer:
Those values can be helpul to find an ideal range for the number of chocolate chips per cookie.
P(5) = 19.82 chips per cookie.
P(95) = 27.38 chips per cookie.
Explanation:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this problem, we have that:
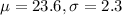
How might those values be helpful to the producer of the chocolate chip cookies?
Those values can be helpul to find an ideal range for the number of chocolate chips per cookie.
P(5)
5th percentile, which is the value of X when Z has a pvalue of 0.05. So it is X when Z = -1.645.


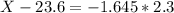
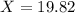
P(5) = 19.82 chips per cookie.
P(95)
95th percentile, which is the value of X when Z has a pvalue of 0.95. So it is X when Z = 1.645.

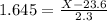
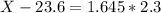

P(95) = 27.38 chips per cookie.