Question

Consider a basketball player spinning a ball on the tip of a finger. If a player performs 2.01J of work to set the ball spinning from rest, at what angular speed ω will the ball rotate? Model a basketball as a thin-walled hollow sphere. For a men's basketball, the ball has a circumference of 0.749 m and a mass of 0.624 kg.

Answer 1

The angular speed of ball is 25.9 rad/s .

Step-by-step explanation:

Given :

Work done by the player , W = 2.01 J .

Mass of hollow spherical ball , m = 0.624 kg .

Circumference of hollow spherical ball , C = 0.749 m .

Therefore , its radius is ,

`r=(C)/(2\pi)\\\\r=(0.749 )/(2\pi)\\\\r=0.12\ m`

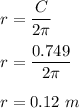
Now , this work done must be equal to the rotational energy of the ball .

We know ,

`U=(I \omega^2)/(2)`

Therefore ,

`\omega=\sqrt{(2U)/( I )}\\\\\omega=\sqrt{(2U)/( (2MR^2 )/(3) )}\\\\\omega=\sqrt{(3U)/( MR^2)}\\\\\omega=\sqrt{(3* 2.01)/(0.624 * 0.12^2)}\\\\\omega=25.9\ rad/s`

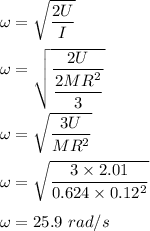
Hence , this is the required solution .