Answer: The minimum value of the potential difference through which these ions must be accelerated is
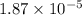 MV.
MV.
Step-by-step explanation:
The given data is as follows.
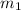 = 35 amu
= 35 amu
=
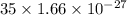
= kg
= 37 amu
=
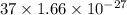
= kg
It is known that,
work done on charged particle = gain in kinetic energy
So,
v =
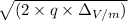
A centripetal force is experienced when charged particles enter a uniform magnetic field.
Hence, F =
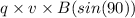
![\frac{m * (v^(2))/(r) = q * v * B]()
r =
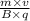
And,
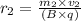
On completion of semi circle, the distance between two paths =
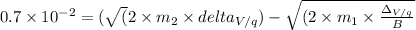
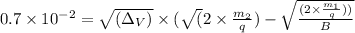
![√((\Delta_V)) = 0.7 * 10^(-2) * \frac{B}{(\sqrt{(2 * \frac{m_(2){q})} - \sqrt{((2 * m_(1))/(q)))}]()
=
![\frac{0.7 * 10^(-2) * 1.2}{(\sqrt{(2 * (6.142 * 10^(-26))/((1.6 * 10^(-19)))}) - \sqrt{(2 * (5.81 * 10^(-26))/((1.6 * 10^(-19))))]()
= 350 volts
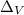 =
=
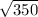
= 18.7 volts
=
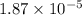 MV
MV
Thus, we can conclude that the minimum value of the potential difference through which these ions must be accelerated is
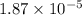 MV.
MV.