Question

If a particle conned to move in one dimension has wavefunction ψ(x), then the probability of nding it between any two points x1 and x2 is: P(x1, x2) = ˆx2 x1 dx |ψ(x)| 2 Calculate the probability of nding a particle between x1 = 0 and x2 = a/3 for the ground-state of a one-dimensional rigid box of size a. [Hint: the calculation involves an integral of the function sin2 θ. Use the identity 2 sin2 θ = 1 − cos 2θ.]

Answer 1

`P(0,a/3)=(1)/(3)-(√(3))/(4\pi)`

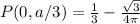
Explanation:

The probability of finding a particle between two points is given by:

`P(x_1,x_2)=\int_(x_1)^(x_2)|\Phi_n|^2dx`

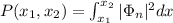
Furthermore, the wave function of a nth state is given by:

`\Phi_n=\sqrt{(2)/(a)}sin((n\pi x)/(a))`

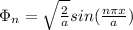
By replacing we obtain

`P(0,(x)/(3))=\int_(0)^{(a)/(3)}(2)/(a)sin^2((n\pi x)/(a))dx`

and by using the relation,

`sin^2\theta=(1)/(2)(1-cos(2\theta))`

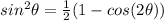
we get for the ground state (n=1):

`P(0,a/3)=((2)/(a))((1)/(2))\int_(0)^{(a)/(3)}(1-cos((2\pi x)/(a)))dx\\\\P(0,a/3)=((2)/(a))((1)/(2))[(a)/(3)-((a)/(2\pi))sin((2\pi (a/3))/(a))]\\\\P(0,a/3)=((1)/(a))[(a)/(3)-((a)/(2\pi))((√(3))/(2))]=(1)/(3)-(√(3))/(4\pi)`

hope this helps!!