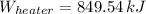Question

A mass of 15 kg of air in a piston-cylinder device is heated from 25 to 77 °C by passing current through a resistance heater inside the cylinder. The pressure inside the cylinder is held constant at 300 kPa during the process, and a heat loss of 60 kJ occurs. Determine the electrical energy supplied

Answer 1

`W_(heater) = 849.54\,kJ`

Step-by-step explanation:

The piston-cylinder system is modelled after the First Law of Thermodynamics:

`W_(heater) - Q_(loss) + U_(1,sys) - U_(2,sys) + W_(1,b) - W_(2,b) = 0`

The electrical energy supplied by the resistance heater is:

`W_(heater) = Q_(loss) + U_(2,sys) - U_(1,sys) + W_(2,b) - W_(1,b)`

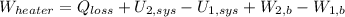
Let suppose that air behaves ideally, so that:

`W_(heater) = Q_(loss) + m\cdot c_(v) \cdot (T_(2)-T_(1)) + m\cdot P\cdot (\\u_(2)-\\u_(1))`

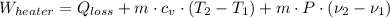
The initial specific volume is determined by the use of the equation of state for ideal gases:

`P \cdot V = n \cdot R_(u)\cdot T`

`P\cdot V = (m)/(M)\cdot R_(u)\cdot T`

`P\cdot \\u = (R_(u)\cdot T)/(M)`

`\\u = (R_(u)\cdot T)/(P\cdot M)`

`\\u_(1) = (\left(8.314\,(kPa\cdot m^(2))/(kmol\cdot K)\right)\cdot (298.15\,K))/((300\,kPa)\cdot (28\,(kg)/(kmol) ))`

`\\u_(1) = 0.295\,(m^(3))/(kg)`

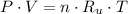
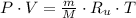
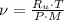
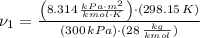
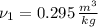
The final specific volume can be derived from the following relationship:

`(\\u_(2))/(T_(2)) = (\\u_(1))/(T_(1))`

`\\u_(2) = (T_(2))/(T_(1))\cdot \\u_(1)`

`\\u_(2) = (350.15\,K)/(298.15\,K) \cdot (0.295\,(m^(3))/(kg) )`

`\\u_(2) = 0.346\,(m^(3))/(kg)`

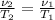
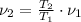
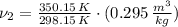
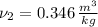
The energy supply is:

`W_(heater) = 60\,kJ + (15\,kg)\cdot \left[\left(0.718\,(kJ)/(kg\cdot ^(\textdegree)C) \right)\cdot (77\,^(\textdegree)C- 25\,^(\textdegree)C) + (300\,kPa)\cdot \left(0.346\,(m^(3))/(kg)-0.295\,(m^(3))/(kg) \right)\right]`
`W_(heater) = 849.54\,kJ`