Answer:
(a) 0.13567
(b) 0.68023
Complete Problem Statement:
Suppose the heights (in inches) of men ages (20-29) in the United States are normally distributed with a mean of 69.3 inches and a standard deviation of 2.92 inches. A study participant is randomly selected
Find the probability that his height is :
(a) Less than 66 inches
(b) Between 66 inches and 72 inches
Explanation:
To find the probability, we will need to calculate the Z-Score.
The formula for which is :
z = (X-μ) / σ
X= raw score
μ= mean
σ = Standard Deviation
(a) Probability that the height of participant is less than 66 inches:
First we find value of z :
z =
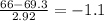
Use this to look up at probability table, we get:
Probability (at z equals -1.1 ) = 0.13567
(b) Probability that the height of participant is between 66 inches and 72 inches
First we find value of z for X=72 inches :
z =
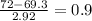
Probability ( at z equals 0.9) = 0.8159
We already have value of z for X=66 inches , which is z = -1.1 with Probability (at z equals -1.1 ) = 0.13567
Since we are asked for probability between 66 inches and 72 inches, we subtract the two probabilities , such that:
Probability (at h=72) - Probability (at h=66) = 0.8159-0.13567=0.68023
Probability that height of participant is between 66 inches and 72 inches =0.68023