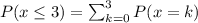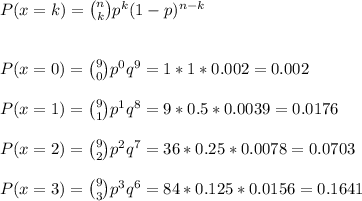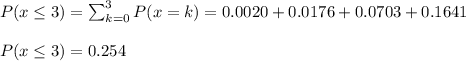Question

A hair stylist has been in business one year. Fifty percent of his customers are walk-in business. If he randomly samples nine of the people from last week’s list of customers, what is the probability that three or fewer were walk-ins? If this outcome actually occurred, what would be some of the explanations for it?

Answer 1

The probability that three or fewer were walk-ins is P=0.254.

If this outcome occured, it can be produced by pure chance, as it nos a very unlikely event, although the expected number of walkins is 4.5.

Explanation:

This problem can be modeled as a binomial experiment, with p=0.5 and n=9.

p is the probability that the customers are walk-ins.

n is the sample size.

We have to calculate the probabilty that three or fewer are walk-ins.

`P(x\leq3)=\sum_(k=0)^3P(x=k)`

`\\ P(x=k)=\binom{n}{k}p^k(1-p)^(n-k)\\\\\\P(x=0) = \binom{9}{0} p^(0)q^(9)=1*1*0.002=0.002\\\\P(x=1) = \binom{9}{1} p^(1)q^(8)=9*0.5*0.0039=0.0176\\\\P(x=2) = \binom{9}{2} p^(2)q^(7)=36*0.25*0.0078=0.0703\\\\P(x=3) = \binom{9}{3} p^(3)q^(6)=84*0.125*0.0156=0.1641\\\\`

`P(x\leq3)=\sum_(k=0)^3P(x=k)=0.0020+0.0176+0.0703+0.1641\\\\P(x\leq3)=0.254`