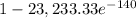Answer:
For the three polices,
The means are :
10,000(0.01) = 100
20,000(0.02) = 400
40,000(0.03) = 1,200
Because the Poisson variance is equal to the mean, the variances are
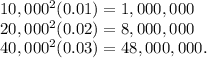
The overall mean is
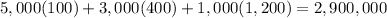
and the variance is
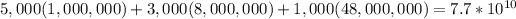
Total claims are the sum of 9,000 compound Poisson distributions which itself is a compound Poisson distribution with
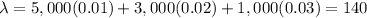
and the severity distribution places probability 50/140 on 10,000, 60/140 on 20,000, and 30/140 on 40,000. Using the recursive formula with units of 10,000,
P(S=0)=e
For the three polices, the means are
10,000(0.01) = 100, 20,000(0.02) = 400, and 40,000(0.03) = 1,200.
Because the Poisson variance is equal to the mean, the variances are
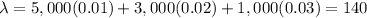
The overall mean is
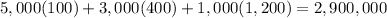 and the variance is
and the variance is
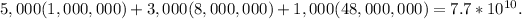
Total claims are the sum of 9,000 compound Poisson distributions which itself is a compound Poisson distribution with
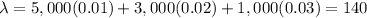 and the severity distribution places probability 50/140 on 10,000, 60/140 on 20,000, and 30/140 on 40,000. Using the recursive formula with units of 10,000
and the severity distribution places probability 50/140 on 10,000, 60/140 on 20,000, and 30/140 on 40,000. Using the recursive formula with units of 10,000

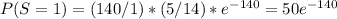
![P(S=2)=140/2[(5/14)*50*e^(-140)+(2*6/14)e^(-140)]=1310e^(-140)](https://img.qammunity.org/2021/formulas/mathematics/high-school/ejf61bva1pgjwuqi1pwxwyd02aflmbi27h.png)
![P(S=3)=140/3[(5/14)*1,310e^(-140)+(2*6/14)e^(-140)]=21,873.33e^(-140)](https://img.qammunity.org/2021/formulas/mathematics/high-school/8c502zrnhv0ujx0qxql5t567eguntw1ls7.png)
P(S > 3) = 1 - P (S ≤ 3)
=