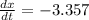Answer:
According to the information of the problem x = 15 , p=2.90 and dp/dt = -1.15
then
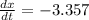
Explanation:
Since everything is changing with respect to time and
 are related according to the following equation
are related according to the following equation

We need to find the implicit derivative with respect to the time. And we get the following.

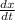 is what we don't know, so we solve for it and get
is what we don't know, so we solve for it and get
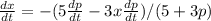
Now. According to the information of the problem x = 15 , p=2.90 and dp/dt = -1.15
then