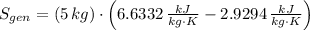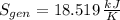Question

A well-insulated rigid tank contains 5 kg of a saturated liquid–vapor mixture of water at 200 kPa. Initially, three-quarters of the mass is in the liquid phase. An electric resistance heater placed in the tank is now turned on and kept on until all the liquid in the tank is vaporized. Determine the entropy change of the steam during this process. Use steam tables.

Answer 1

`S_(gen) = 18.519\,(kJ)/(K)`

Step-by-step explanation:

Given that rigid tank is a closed system, the following model is constructed after the First Law of Thermodynamics:

`W_(heater) + U_(sys,1) - U_(sys,2) = 0`

`W_(heater) = U_(sys,2) - U_(sys,1)`

`W_(heater) = m\cdot (u_(2)-u_(1))`

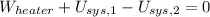
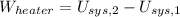
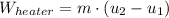
The entropy generation inside the rigid tank is determined by appropriate application of the Second Law of Thermodynamics:

`S_(sys,1) - S_(sys,2) + S_(gen) = 0`

`S_(gen) = S_(sys,2) - S_(sys,1)`

`S_(gen) = m\cdot (s_(2)-s_(1))`

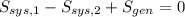
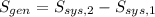
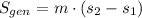
The properties of the steam are obtained from steam tables:

Intial State

`P = 200\,kPa`

`T = 120.21\,^(\textdegree)C`

`\\u = 0.2222\,(m^(3))/(kg)`

`u = 1010.7\,(kJ)/(kg)`

`s = 2.9294\,(kJ)/(kg\cdot K)`

`x = 0.25`

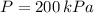
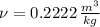
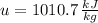
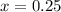
Final State

`P = 869.567\,kPa`

`T = 173.88\,^(\textdegree) C`

`\\u = 0.2222\,(m^(3))/(kg)`

`u = 2578.6\,(kJ)/(kg)`

`s = 6.6332\,(kJ)/(kg\cdot K)`

`x = 1.00`

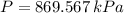
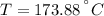
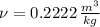
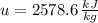
The entropy change of the steam during the process is:

`S_(gen) = (5\,kg)\cdot \left(6.6332\,(kJ)/(kg\cdot K) - 2.9294\,(kJ)/(kg\cdot K) \right)`

`S_(gen) = 18.519\,(kJ)/(K)`