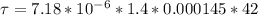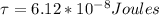Question

A circular loop of radius 14 cm carries a current of 16 A. A flat coil of radius 0.68 cm, having 42 turns and a current of 1.4 A, is concentric with the loop. The plane of the loop is perpendicular to the plane of the coil. Assume the loop's magnetic field is uniform across the coil. What is the magnitude of (a) the magnetic field produced by the loop at its center and (b) the torque on the coil due to the loop?

Answer 1

a

The magnitude of magnetic field is
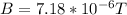
`B=7.18*10^(-6)T`

b

The torque is
`\tau= 6.12*10^(-8) Joules`

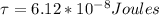
Step-by-step explanation:

From the question we are told that

The radius of the circular loop is
`r = 14 \ cm = (14)/(100) = 0.14 m`

The current carried by the circular loop is
`I_l = 16A`

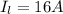
The radius of the flat loop is
`r_f = 0.68cm = (0.68)/(100) = 0.0068m`

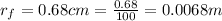
The current carried by the flat loop
`I_f =1.4A`

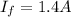
The magnitude magnetic field produce at the center due to the circular loop is mathematically represented as

`B = (\mu_o I_i)/(2 * r)`

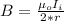
Where
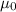`\mu_0` is the permeability of free space with a value of
`\mu = 4 \pi *10^(-7) H/m`

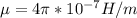
Substituting values

`B= (4\pi *10^(-7) * 16)/(2(1.4))`

`B=7.18*10^(-6)T`

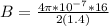
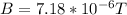
The torque on the coil due to the loop is mathematically represented as

`\tau = BIAN`

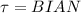
Where A is the area and it is evaluated as

`A = \pi r^2`

`=3.142 * 0.0068^2`

`=0.000145m^2`

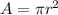
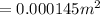
N is the number of turns with value N = 42 turns

No substituting values into the equation for torque

`\tau = 7.18*10^(-6) * 1.4 * 0.000145 *42`

`\tau= 6.12*10^(-8) Joules`