Answer:
80% confidence interval for the difference in two proportions is [0.055 , 0.105].
Explanation:
We are given that a telephone service representative believes that the proportion of customers completely satisfied with their local telephone service is different between the Northeast and the Midwest.
The survey included a random sample of 1200 northeastern residents and 1280 mid western residents. 44% of the northeastern residents and 36% of the mid western residents reported that they were completely satisfied with their local telephone service.
Firstly, the pivotal quantity for 80% confidence interval for the difference in two proportions is given by;
P.Q. =
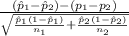 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of northeastern residents who were completely satisfied with their local telephone service = 0.44
= sample proportion of northeastern residents who were completely satisfied with their local telephone service = 0.44
 = sample proportion of mid western residents who were completely satisfied with their local telephone service = 0.36
= sample proportion of mid western residents who were completely satisfied with their local telephone service = 0.36
 = sample of northeastern residents = 1200
= sample of northeastern residents = 1200
 = sample of mid western residents = 1280
= sample of mid western residents = 1280
 = true proportion of northeastern residents who were completely satisfied with their local telephone service
= true proportion of northeastern residents who were completely satisfied with their local telephone service
 = true proportion of mid western residents who were completely satisfied with their local telephone service
= true proportion of mid western residents who were completely satisfied with their local telephone service
Here for constructing 80% confidence interval we have used Two-sample z proportion statistics.
So, 80% confidence interval for the difference in two proportions,
 is ;
is ;
P(-1.2816 < N(0,1) < 1.2816) = 0.80 {As the critical value of z at 10% level of
significance are -1.2816 & 1.2816}
P(-1.2816 <
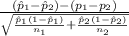 < 1.2816) = 0.80
< 1.2816) = 0.80
P(
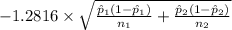 <
<
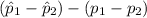 <
<
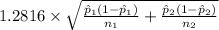 ) = 0.80
) = 0.80
P(
 <
<
 <
<
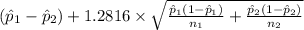 ) = 0.80
) = 0.80
80% confidence interval for
 =
=
[
 ,
,
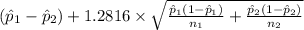 ]
]
= [
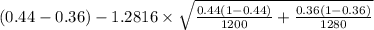 ,
,
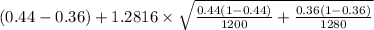 ]
]
= [0.055 , 0.105]
Therefore, 80% confidence interval for the difference in two proportions is [0.055 , 0.105].