Question

A simple pendulum, consisting of a mass on a string of length L, is undergoing small oscillations with amplitude A.

1. The mass is increased by a factor of four. What is true about the period?
Choose the best answer.
a. The period is halved.
b. The period increases by a factor of four.
c. The period remains unchanged.
d. The period doubles.
e. The period decreases by a factor of four.

Answer 1

C

Step-by-step explanation:

Mass doesn't affect period

Answer 2

A. Period is halved

Step-by-step explanation:

The period of a pendulum swing, T, is given in terms of mass as:

`T = 2\pi \sqrt{(I)/(mgL) }`

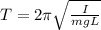
where I = moment of inertia

m = mass of the pendulum

g = acceleration due to gravity

h = Length of string

If the mass is increased by a factor of 4, that means:

M = 4m

(M = new mass)

The new period of the pendulum,
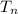`T_n`, will now be:

`T_n = 2\pi \sqrt{(I)/(MgL) }\\\\\\T_n = 2\pi \sqrt{(I)/(4mgL) }\\\\\\T_n = 2\pi \sqrt{(1)/(4) * (I)/(mgL) }\\\\\\T_n = (2\pi)/(2) \sqrt{(I)/(mgL) }\\\\\\T_n = (1)/(2) * 2\pi \sqrt{(I)/(mgL) }\\\\\\T_n = (1)/(2) * T`

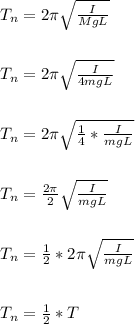
Hence, the period is halved.