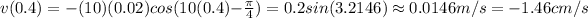Answer and Explanation:
For one-dimensional simple harmonic motion, the equation of motion is given by:
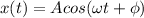
Where:

Also, you may know the following basic equations:
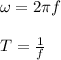
Where:
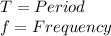
and:
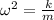
Where:
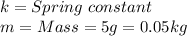
Let's solve the problem using the previous information. As you can see, most of the questions can be solve by extracting directly the data from the equation provided by the problem.
a. The amplitude:
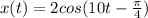
As you can see the amplitude is:
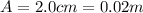
b. The period.
Let's isolate f from this equation:
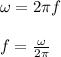
The angular frequency in this case is 10 so:
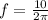
Since the period is the inverse of the frequency:
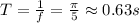
c. The spring constant.
Using the data provided and the equation:
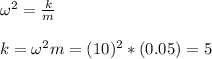
d. The phase constant.
From the equation provided:
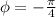
e. The initial conditions.
Let's evaluate the function for t=0:

f. The maximum speed.
As you may know the velocity is the derivative of the position, so:
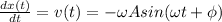
And the acceleration is the derivative of the velocity, so:
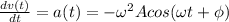
From the basic notions of calculus, the velocity is maximum when the acceleration is 0, so we need to find for which t the acceleration is 0. Once we find that value, we just need to evaluate it into the velocity equation:
The cosine is zero for:
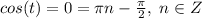
So:
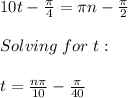
For n=1:
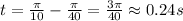
Therefore the maximum speed is:
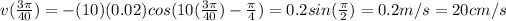
g. The total energy.
The elastic potential Energy is given by the next equation:

Now, we need to find the maximum displacement from the equilibrium point. Which is when the velocity is 0:
The sine function is 0 when:

So:
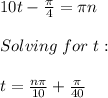
For n=1:
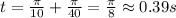
Therefore the maximum displacement is:
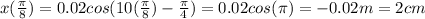
So, the total energy is:
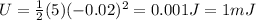
h. The velocity at t = 0.40 s.
Simply evaluate the velocity at t=0.40s