Question

The daily cost of producing x high performance wheels for racing is given by the following​ function, where no more than 100 wheels can be produced each day. What production level will give the lowest average cost per​ wheel? What is the minimum average​ cost?

C(x)=0.03x^3-4.5x^2+171x; (0,100]

Answer 1

The production of wheel per day is 74 which gives lowest average cost per wheel.

The minimum average cost is $168.72.

Explanation:

Given function of average cost is

`C(x)= 0.03x^3-4.5x^2+171x`

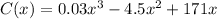
Differentiating with respect to x

C'(x)= 0.09 x² -9.0 x+171

Again differentiating with respect to x

C''(x) = 0.18 x -9.0

To find the minimum average cost, first we have to set C'=0.

The function's slope is zero at x=a, and the second derivative at x=a is

• less than 0, it is critical maximum.

• greater than 0, it is critical minimum.

Now ,

C'=0

⇒ 0.09 x² -9.0 x+171=0

⇒x = 74.49, 25.50

`C''(x)|_(x=74.49) = 0.18 (74.49)-9.0=4.41>0`

`C''(x)|_(x=25.50) = 0.18 (25.50)-9.0=-4.41<0`

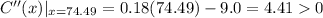
Therefore at x= 74.49≈ 74, the average cost is minimum.

The production of wheel per day is 74 which gives lowest average cost per wheel.

The minimum average cost
`C(x)= 0.03x^3-4.5x^2+171x`

`=(0.03 * 74^3)-(4.5 * 74^2)+(171* 74)`

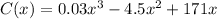
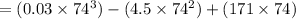
=168.72

[Assume the average cost is in dollar]

The minimum average cost is $168.72.