Answer:

Explanation:
We have been that on a standardized exam, the scores are normally distributed with a mean of 200 and a standard deviation of 10. We are asked to find the z-score of a person who scored 181 on the exam.
We will use z-score formula to solve our given problem.
 , where,
, where,
z = z-score,
x = Random sample score,
 = Mean,
= Mean,
 = Standard deviation.
= Standard deviation.
Upon substituting our given values in above formula, we will get:
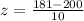
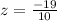

Therefore, the z-score of the person would be
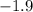 .
.