Answer:
$1003.92
Step-by-step explanation:
The invoice price is calculated as the reported price plus the accrued interest. Therefore, the formula for accrued interest is shown below:
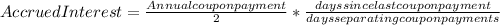
Given that the coupon rate is 8%, therefore the bond pays $80 of coupon payments every year.
January 14 was the day that the last coupon was paid, so it has been 14 days since the last payment.
The coupon period is 182 days.
Therefore, the accrued interest is

The invoice price is calculated as:
$1000.625 + $3.297
= $1003.922.
Therefore the invoice price of the bond is $1003.92