Question

Consider atmospheric air at 20°C and a velocity of 30 m/s flowing over both surfaces of a 1-m-long flat plate that is maintained at 130°C. Determine the rate of heat transfer per unit width from the plate for values of the critical Reynolds number corresponding to 105 , 5 × 105, and 106 .

Answer 1

`At 10^5 = 17270W/m`

`At 5*10^5 = 13127.84 W/m`

`At 10^6 = 8472.2 W/m`

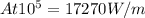
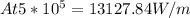
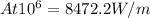
Step-by-step explanation:

We are given:

T_o = 20°C

Flat plate temp, T_s = 230°C

v = 30m/s

Let's find the mean:

`T_f = (20+130)/(2)`

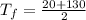
= 75°C

Using air table at 75°C at 1 atm pressure, we have:

`Thermal conductivity, k = 29.66*10^-^3 W/m•K`

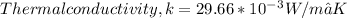
Prandtl number, Pr = 0.7087

`Viscosity, v= 20.82*10^-^6 m^2/s`

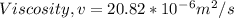
Calculating Reynolds number, we have:

`Re_L = (VL)/(v)`

`Re_L = (30*1)/(20.82*10^-^6)`

`= 1.44*10^6`

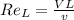
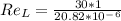
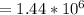
Since the Reynolds number is higher than the critical Reynolds number, we can say there is a turbulent flow.

Therefore we'll now use the formula:

`Nu_L = (0.037Re_L^0^.^8 - A)Pr^0^.^3^3`

`For Re_x = 10^5`

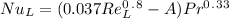
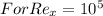
To get A using the formula, we have:

`A = 0.037(10^5) - 0.664(10^5)^0^.^5`

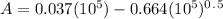
= 160.024

`To find Nu_L`

`Nu_L =(0.037(1.44*10^6)^0^.^8-160.024)(0.7087)^0^.^3^3`

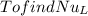
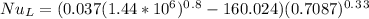
= 2646.78

Connective heat transfer:

`h_L = (Nu_L K)/(L)`

`=((2646.78)(2966*10^-^3))/(1)`

`=78.50W/m^2•K`

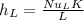
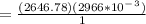
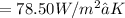
Lets calc for heat transfer:

`q_1_0_^_5 = 2h_L L(T_s-T_o)`

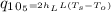
= 2(78.50)(1)(130-20)

= 1720W/m

`For Re_x = 5*10^5`

`A = 0.037Re_x^0^.^8-0.664Re_x^0^.^5`

`= 0.037(5*10^5)^0^.^8-0.664(5*10^5)^0^.^5`

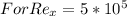
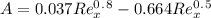
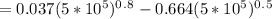
= 871.323

Calculating Nu_L we have:

`h_L =(Nu_L K)/(L)`

`= (2011.88*29.66*10^-^3)/(1)`

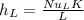
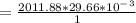
= 59.672W/m²•K

For the heat transfer:

`q_5_*_1_0_^5 = 2(59.672)(1)(130-20)`

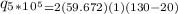
= 13127.84W/m

`For Re_x = 10^6`

`A= 0.037(10^6)^0^.^8-0.664(10^6)^0^.^5`

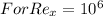
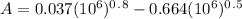
= 1670.54

Calculating Nu_L:

`Nu_L = (0.037(1.44*10^6)^0^.^8-1670.54)(0.7087)^0^.^3^3`

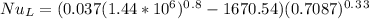
= 1298.51

Calculating the convective heat transfer coefficient:

`h_L = (Nu_L*k)/(L)`

`((1298.51)(29.66*10^-^3))/(1)`

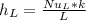
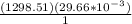
=38.51 W/m²•K

To calculte for rate of heat transfer, we have:

`q_1_0_^6=2h_LL(T_s-T_o)`

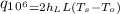
=2(38.51)(1)(130-20)

= 8472.2W/m