Question

A motorcycle, which has an initial linear speed of 9.8 m/s, decelerates to a speed of 2.2 m/s in 3.4 s. Each wheel has a radius of 0.65 m and is rotating in a counterclockwise (positive) directions. What is (a) the constant angular acceleration (in rad/s2) and (b) the angular displacement (in rad) of each

Answer 1

The angular acceleration and angular displacement is
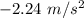`-2.24\ m/s^2` and 31.34 rad .

Step-by-step explanation:

Given :

Initial linear speed , u = 9.8 m/s .

Final speed , v = 2.2 m/s .

Time taken , t = 3.4 s .

Radius of wheel , r = 0.65 m .

So , decelerates of wheel is given by :

`v-u=at\\2.2-9.8=a* 3.4\\a=-2.24\ m/s^2`

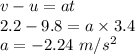
Therefore , angular velocity is given by :

`\omega=(a)/(r)\\\\\omega=(-2.24)/(0.65)\\\\\omega =-3.45\ rad/s^2`

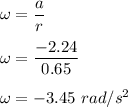
Now , linear displacement is :

`s=ut+(at^2)/(2)\\\\s=9.8* 3.4+(-2.24* 3.4^2)/(2)\\\\s=20.37\ m`

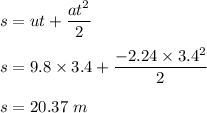
Therefore , angular displacement is :

`d=(s)/(r)\\\\d=(20.37)/(0.65)\\\\d=31.34\ rad`

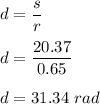
Hence , this is the required solution .