Question

Airline passengers arrive randomly and independently at the passenger-screening facility at a major international airport. The mean arrival rate is 6 passengers per minute. Compute the probability of no arrivals in a one-minute period (to 6 decimals).

Answer 1

0.002478 is the probability of no arrivals in a one-minute period.

Explanation:

We are given the following information in the question:

Mean arrival rate = 6 passengers per minute.

`\lambda = 6`

The airline passengers can be treated as a Poisson distribution.

Poisson distribution.

• The Poisson distribution is the discrete probability distribution of the number of events occurring in a given time period, given the average number of times the event occurs over that time period.

Formula:

`P(X =k) = \displaystyle(\lambda^k e^(-\lambda))/(k!)\\\\ \lambda \text{ is the mean of the distribution}`

P( no arrivals in a one-minute period)

`P( x =0) \\\\= \displaystyle(6^0 e^(-6))/(0!)= 0.002478`

0.002478 is the probability of no arrivals in a one-minute period.

Answer 2

The probability of no arrivals in a one-minute period is 0.002479.

Explanation:

We are given that Airline passengers arrive randomly and independently at the passenger-screening facility at a major international airport. The mean arrival rate is 6 passengers per minute.

The above situation can be represented through Poisson distribution because a random variable which includes the arrival rate is considered as Poisson random variable.

The Probability distribution function for Poisson random variable is ;

`P(X=x) = (e^(-\lambda )* \lambda^(x) )/(x!) ;x=0,1,2,3,.....`

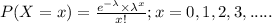
where,
`\lambda` = arrival rate

Let X = Arrival of Airline passengers

The mean of the Poisson distribution is given by = E(X) =
`\lambda`, which is given to us as 6 passengers per minute.

So, X ~ Poisson (
`\lambda=6`)

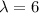Now, the probability of no arrivals in a one-minute period is given by = P(X = 0)

P(X = 0) =
`(e^(-6)* 6^(0) )/(0!)`

=
`e^(-6)`

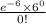
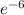
= 0.002479

Hence, the probability of no arrivals in a one-minute period is 0.002479.