Question

A bomb is initially at rest when it suddenly explodes into three pieces. A 5-kg piece goes north at 6 m/s, and a 2-kg piece goes east at 20 m/s. The speed of the third piece is 25 m/s. What is the mass of the third piece

Answer 1

The mass of the third piece is 2kg.

Step-by-step explanation:

From the conservation of linear momentum, we know that the total initial momentum must be equal to the total final momentum. Since the bomb is initially at rest, its initial momentum is zero. And as momentum is a vector quantity, we have to study each component by separate. Let's name the piece of 5-kg piece A, the piece of 2-kg piece B and the piece of unknown mass piece C.

Now, we know that the momentum in each direction must be conserved (in this case, equal to zero). So, we can consider the momentum in the direction of the piece C; the momentum of piece C has to be equal and opposite to the vectorial sum of momenta of piece A and piece B. And, since those momenta are perpendicular to each other, we can say that:

`p_C=\sqrt{p_A^(2)+p_B^(2)}\\\\m_Cv_C=\sqrt{(m_Av_A)^(2)+(m_Bv_B)^(2)}\\\\m_C=\frac{\sqrt{(m_Av_A)^(2)+(m_Bv_B)^(2)}}{v_C}`:

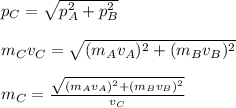Then, plugging in the given values, we obtain:

`m_C=\frac{\sqrt{(5kg)^(2)(6m/s)^(2)+(2kg)^(2)(20m/s)^(2)}}{25m/s}\\\\m_C=2kg`

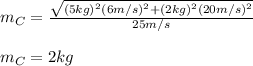
It means that the mass of the third piece is 2kg.