Question

Suppose the lifetime, in years, of a motherboard is modeled by a Gamma distribution with parameters α=80 and λ=4. Use the Central Limit Theorem to approximate the probability that the motherboard of a new computer will last for at least the next 15 years.

Answer 1

Therefore there's a 99.99% probability the motherboard of your new computer will last for at least 15 years.

Explanation:

This is the general idea to solve the problem.

Suppose that the mean and variance of the your distribution are .
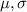`\mu , \sigma` respectively. Then, according to the problem you are looking for the probability.

`P(X \geq 15) = 1 - P(X <15) = 1 - (P(X=0)+P(X=1) + .....+P(X=14))`

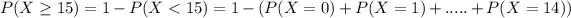
Consider then the following random variable.

`T = X_1 + X_2 + .... + X_(14)`

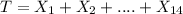
Using the central limit theorem
`T` distribution will be close to normal, and its mean and variance will be
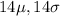`14\mu , 14\sigma` , respectively. Therefore you just have to find the probability that a normally distributed random variable with that mean and that variance which I just mentioned is less than 14.

For this case we have that

`\mu = \alpha / \gamma = 20 \\\sigma = \alpha(\alpha+1) / \gamma^2 - (\alpha/ \gamma)^2 = 5`

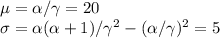
Then you have that

`14\mu = 280\\14\sigma = 70\\`

and we have that if
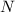`N` is a normally distributed random variables with mean 280 and variance 70 we have that

`P(N \leq 14 ) = 0.0001`

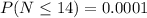
the actual probability we are looking for is

`1-P(N\leq14) = 1-(0.0001) = 0.9999`

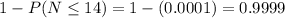
Therefore there's a 99.99% probability the motherboard of your new computer will last for at least 15 years.