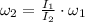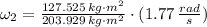Answer:

Step-by-step explanation:
Let assume that circular platform is a solid cylinder. Given the absence of external forces, the situation can be analyzed by applying the Principle of Angular Momentum, which states that:
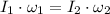
The initial moment of inertia is:
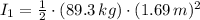
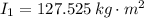
Likewise, the final moment of inertia is:
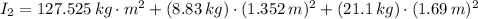
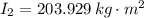
The final angular speed is: