Question

Suppose that 10% of all students at Cooley High play a winter sport, that 20% play a spring sport, and that 5% play both a winter and a spring sport. What is the probability that a randomly chosen student plays a winter or a spring sport?

a. 30%
b. 25%
c. 35%
d. 20%
e. None of the above

Answer 1

`P_A = 0.1 , P_B = 0.20 , P(A \cap B) = 0.05`

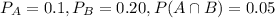
And for this case we want to calculate this probability:

`P(A \cup B)`

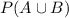
Who represent the probability that a randomly chosen student plays a winter or a spring sport

And for this case we can use the total rule of probability given by:

`P(A \cup B) = P(A) +P(B) -P(A \cap B)`

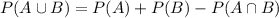
And replacing we got:

`P(A \cup B) = 0.1 +0.2 -0.05 = 0.25`

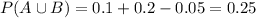
So then the best option for this case would be:

b. 25%

Explanation:

For this case we define the following events:

A = A student selected play a winter sport

B= A student selected play a spring sport

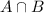`A \cap B`= A student selected play both a winter and a spring sport

And we have the following probabilities associated to the events:

`P_A = 0.1 , P_B = 0.20 , P(A \cap B) = 0.05`

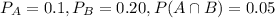
And for this case we want to calculate this probability:

`P(A \cup B)`

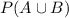
Who represent the probability that a randomly chosen student plays a winter or a spring sport

And for this case we can use the total rule of probability given by:

`P(A \cup B) = P(A) +P(B) -P(A \cap B)`

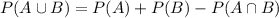
And replacing we got:

`P(A \cup B) = 0.1 +0.2 -0.05 = 0.25`

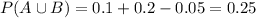
So then the best option for this case would be:

b. 25%

Answer 2

b. 25%

Explanation:

I am going to say that:

A is the probability that a student plays a winter sport.

B is the probability that a student plays a spring sport.

We have that:

`A = a + (A \cap B)`

In which a is the probability that a student plays a winter sport both not a spring sport and
`A \cap B` is the probability that a student plays both a winter and a spring sport.

By the same logic, we have that:

`B = b + (A \cap B)`

5% play both a winter and a spring sport.

This means that
`A \cap B = 0.05`

20% play a spring sport

This means that
`B = 0.2`

10% of all students at Cooley High play a winter sport

This means that
`A = 0.1`

What is the probability that a randomly chosen student plays a winter or a spring sport?

`(A \cup B) = A + B - (A \cap B) = 0.2 + 0.1 - 0.05 = 0.25`

So the correct answer is:

b. 25%