Answer:
the probability that the woman is taller than the man is 0.1423
Explanation:
Given that :
the men's heights are normally distributed with mean
 68
68
standard deviation
 = 3.1
= 3.1
And
the women's heights are normally distributed with mean
 65
65
standard deviation
 = 2.8
= 2.8
We are to find the probability that the woman is taller than the man.
For woman now:
mean
 = 65
= 65
standard deviation
 = 2.8
= 2.8
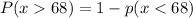
![\\ 1 -p \ P[(x - \mu ) / \sigma < (68-25)/ 2.8]](https://img.qammunity.org/2021/formulas/mathematics/high-school/wysbtk453wmkkpcv2j6ol5s2blcte5qra6.png)
= 1-P (z , 1.07)
Using z table,
= 1 - 0.8577
= 0.1423
Thus, the probability that the woman is taller than the man is 0.1423