Question

A pharmaceutical company has developed a test for a rare disease that is present in 0.5% of the population. The test is 98% accurate in determining a positive result, and the chance of a false positive is 7%. What is the probability that someone who tests positive actually has the disease? (Round your answer to two decimal places.)

Answer 1

The probability that someone who tests positive actually has the disease is P(S|T)=0.43

Explanation:

A pharmaceutical company has developed a test for a rare disease that is present in 0.5% of the population.

The test is 98% a positive result and the chance of a false positive is 7%

To find the probability that someone who tests positive actually has the disease:

Let S be the event that the rare disease present

P(S)=0.05 and

Let T be the event that the test is positive

P(T)=0.98

Then we have to find the Conditional probability
`P(S|T)` :

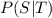By using the formula for Conditional Probability is
`P(A|B)=(P(A and B))/(P(B))`

`P(S|T)=(P(S and T))/(P(S))`

`=((0.05)(0.98))/((0.05)(0.98)+(0.93)(0.07))`

`=(0.049)/(0.049+0.0651)`

`=(0.049)/(0.1141)`

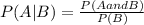
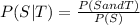
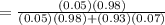
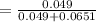
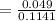
=0.4294

=0.43

∴ P(S|T)=0.43