Question

The only items in a container A are 150 pencils and 725 pens. The ratio of the number of pencils to the number of pens in container B is 2 to 3. If all the pencils and pens in container B are placed in container A, then the ratio of the number of pencils to the number of pens in container A would be 3 to 5. What is the total number of pencils and pens in both container A and container B?

Answer 1

Therefore total number of pencils and pens in container A is 875.

Therefore total number of pencils and pens in container B is 7125.

Explanation:

Given that,

Container A contains 150 pencils and 725 pens.

The ratio of number of the number of pencil to the number of pen in container B is 2:3.

Let the number of pencil and number of pencil in container B be 2x and 3x respectively.

Since all pencils and pen of container B are placed in container A.

So, the number pencil and pen in container A is (150+2x) and (725+3x) respectively.

Now the ratio of pencil to pen is

`=(150+2x)/(725+3x)`

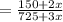
According to the problem,

`(150+2x)/(725+3x)=\frac 35`

`\Rightarrow 5(150+2x)=3(725+3x)`

`\Rightarrow 750+10x=2175+9x`

`\Rightarrow 10x-9x=2175-750`

`\Rightarrow x=1475`

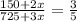
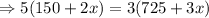
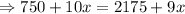
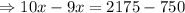
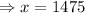
The number pencils in container B is = 2x

=(2×1475)

=2850

The number of pens in container B is = 3x

=(3×1475)

=4425

Therefore total number of pencils and pens in container A is =(150+725)

=875

Therefore total number of pencils and pens in container B is

=(2850+4425)

=7,125