34 years will the account reach $1500, if An initial investment of $1000 is deposited in an account with a 1.2% interest rate, compounded annually.
Explanation:
The given is,
Initial investment of $1000
Interest rate 1.2%, compounded annually
Future amount $1500
Step:1
Formula to calculate the future amount with an interest rate of compounded annually,
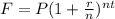 ............................(1)
............................(1)
Where,
F - Future worth amount
P - Initial investment
r - Rate of interest
n - No.of compounding in a year
t - No.of years
From given,
F = $1500
P = $1000
r = 1.2%
n = 1 (compounded annually)
Equation (1) becomes,
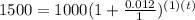
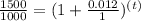
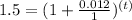
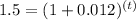
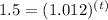
Take log on both sides,

Substitutes log values,
0.17609126 =( t ) 0.0051805
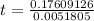
t = 33.99
t ≅ 34 years
Result:
34 years will the account reach $1500, if An initial investment of $1000 is deposited in an account with a 1.2% interest rate, compounded annually.