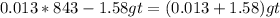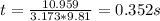Question

A 0.0130-kg bullet is fired straight up at a falling wooden block that has a mass of 1.58 kg. The bullet has a speed of 843 m/s when it strikes the block. The block originally was dropped from rest from the top of a building and had been falling for a time t when the collision with the bullet occurs. As a result of the collision, the block (with the bullet in it) reverses direction, rises, and comes to a momentary halt at the top of the building. Find the time t.

Answer 1

0.352 s

Step-by-step explanation:

Let g = 9.81 m/s2. Then the speed of the block after it's fall down a time t (seconds) before the collision is:

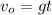`v_o = gt`(0)

Using the law of momentum conservation, the total momentum of the system after the collision must be same as before the collision. Let the upward be the positive direction:

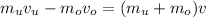`m_uv_u - m_ov_o = (m_u + m_o)v`(1)

where
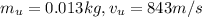`m_u = 0.013 kg, v_u = 843 m/s` are the mass and speed of the bullet prior to the impact.
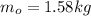`m_o = 1.58 kg` is the mass of the block. v is the speed of the system after the impact. We will focus on v for the next part:

As the system raise and come to a momentarily halt on top of the building (speed at top
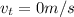`v_t = 0 m/s`), let the vertical distance travel be h (m). We have the following equation of motion

`v_t^2 - v^2 = 2gh`

`0^2 - v^2 = 2gh`

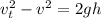
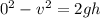
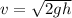`v = √(2gh)`(2)

As h is the same vertical distance that the block has fallen before the collision, we can solve for h in term of t:

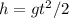`h = gt^2/2`(3)

If we plug eq. (3) into (2):

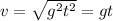`v = √(g^2t^2) = gt` (4)

And plug eq (4) and (0) into eq (1), with all the numbers:

`0.013*843 - 1.58gt = (0.013 + 1.58)gt`

`10.959 = 3.173gt`

`t = (10.959)/(3.173*9.81) = 0.352 s`