Question

A 46.50 mL aliquot from a 0.470 L solution that contains 0.435 g of MnSO 4 ( MW = 151.00 g/mol) required 41.9 mL of an EDTA solution to reach the end point in a titration. What mass, in milligrams, of CaCO 3 ( MW = 100.09 g/mol) will react with 1.88 mL of the EDTA solution?

Answer 1

`m_(CaCO_3)=1.28x10^(-3)gCaCO_3`

Step-by-step explanation:

Hello,

In this case, for the first titration, the molarity of the MnSO₄ is:

`M_(MnSO_4)=(0.435g*(1mol)/(151g) )/(0.470L)=6.13x10^(-3)M`

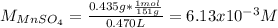
Now, the moles that are neutralized by the EDTA for the 45.50-mL aliquot are:

`n_(MnSO_4)=6.13x10^(-3)(mol)/(L) *0.0465L=2.85x10^(-4)mol`

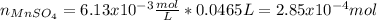
In such a way, those moles equals the EDTA moles based on the titration main equation:

`n_(MnSO_4)=n_(EDTA)`

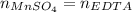
Next, the concentration of the EDTA 41.9-mL solution is:

`M_(EDTA)=(2.85x10^(-4)mol)/(0.0419L)=6.80x10^(-3)M`

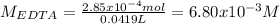
Afterwards, for the second titration, the moles of EDTA that equal the neutralized grams of calcium carbonate are:

`n_(EDTA)^{2^(nd) titration}=6.80x10^(-3)(mol)/(L) *0.00188L=1.28x10^(-5)mol`

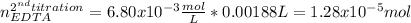
Finally, the grams of calcium carbonate turn out:

`n_(CaCO_3)=n_(EDTA)^{2^(nd)titration}=1.28x10^(-5)mol\\m_(CaCO_3)=1.28x10^(-5)mol*(100.09g)/(1mol) \\m_(CaCO_3)=1.28x10^(-3)gCaCO_3`

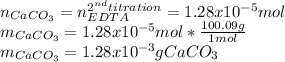
Best regards.