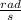Question

During a trampoline routine, a gymnast is tumbling in the air at 20 rad/s in a tuck position. He then extends into a layout position and doubles his radius of gyration just before landing on the trampoline bed. How fast is his angular velocity at this instant, just before landing on the trampoline bed?

Answer 1

The angular velocity just before landing on the trampoline bed is 5
`(rad)/(s)`

Step-by-step explanation:

Given:

Angular speed of gymnast
`\omega _(1) = 20(rad)/(s)`

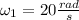
From the formula of radius of gyration,

`R = \sqrt{(I)/(A) }`

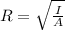
Where
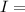`I =` moment of inertia

`I = AR^(2)`

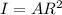
According to the conservation of angular momentum,

`I_(1) \omega _(1) = I_(2) \omega _(2)`

`AR_(1) ^(2) \omega _(1) = A R_(2) ^(2) \omega _(2)`

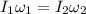
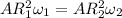
Here radius of gyration is double,

`R_(2) = 2 R_(1)`

So we can write,

`R_(1)^(2) \omega _(1) = 4R_(1)^(2) \omega _(2)`

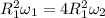
For finding the angular velocity just before landing,

`\omega _(2) = (\omega _(1) )/(4)`

`\omega _(2) = (20)/(5)`

`\omega _(2) = 5(rad)/(s)`

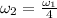
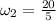
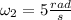
Therefore, the angular velocity just before landing on the trampoline bed is 5
`(rad)/(s)`