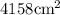Answer:
Explanation:
GIVEN: A cone has a circular base, a perpendicular height of
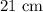 and a semi vertical angle of
and a semi vertical angle of
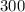 .
.
TO FIND: Calculate the slant height of the cone. Find the area of its base.
SOLUTION:
Consider the figure attached.
Let the radius of cone be

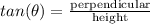
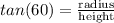
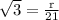
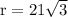
Now,
area of base
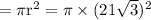
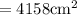
Hence Area of base of cone is