Question

A researcher is interested in comparison of male and female students of Rutgers University in terms of how many hours they study per week. She collects data from 138 female and 115 male students of Rutgers, performs hypothesis testing and finds Z value of 2.86. What conclusion she can make if level of significance is 2%?

Answer 1

Explanation:

Hello!

The researcher is interested in comparing how many hours per week the students dedicate to studying regarding their gender.

Let 1 denote the females and 2 denote the males, the parameter of interest will be the difference between the average weekly study hours of female students and the average weekly hours of study of male students, symbolically:

μ₁ - μ₂

If the objective is to see if there is any difference between the average weekly study hours, the statistical hypotheses are:

H₀: μ₁ - μ₂ = 0

H₁: μ₁ - μ₂ ≠ 0

α: 0.02

The calculated statistic is
`Z_(H_0)`= 2.86

This Hypothesis test is two-tailed, meaning that the rejection region is divided in two tails, using the critical value approach:

`Z_(\alpha /2)= Z_(0.01)= -2.334`

`Z_(1-\alpha /2)= Z_(1-0.01)= Z_(0.99)= 2.334`

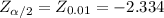
The decision rule is:

If
`Z_(H_0)` ≤ -2.334 or if
`Z_(H_0)`≥2.334, then you reject the null hypothesis.

If -2.334 <
`Z_(H_0)` < 2.334, then you do not reject the null hypothesis.

`Z_(H_0)` is greater than the upper critical value, so the decision is to reject the null hypothesis.

Then using a 2% significance level, the test is significant, you can conclude that the population mean weekly study hours of female students and the population mean weekly hours of study of male students are different.

I hope this helps!