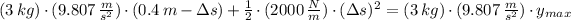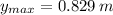Question

A metal block of mass 3 kg is falling downward and has velocity of 0.44 m/s when it is 0.8 m above the floor. It strikes the top of a relaxed vertical spring of length 0.4 m. The spring constant is 2000 N/m. After striking the spring, the block rebounds. What is the maximum height above the floor that the block reaches after the impact

Answer 1

0.81 m

Step-by-step explanation:

In all moment, the total energy is constant:

Energy of sistem = kinetics energy + potencial energy = CONSTANT

So, it doesn't matter what happens when the block hit the spring, what matters are the (1) and (2) states:

(1): metal block to 0.8 m above the floor

(2): metal block above the floor, with zero velocity ( how high, is the X)

Then:

`E_(kb1) + E_(gb1) = E_(kb2) + E_(gs2)`

`E_(kb1) + E_(gb1) = 0 + E_(gs2)`

`(1)/(2)*m*V_(b1) ^(2) + m*g*H_(b1) = m*g*H_(b2)`

`H_(b2) = (V_(b1) ^(2) )/(2g) + H_(b1)`

Replacing data:

`H_(b2) = (0.44^(2) )/(2*9.81) + 0.8`

`H_(b2) = (0.44^(2) )/(2*9.81) + 0.4`

HB2 ≈ 0.81 m

Answer 2

`y_(max) = 0.829\,m`

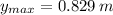
Step-by-step explanation:

Let assume that one end of the spring is attached to the ground. The speed of the metal block when hits the relaxed vertical spring is:

`v = \sqrt{(0.8\,(m)/(s))^(2) + 2\cdot (9.807\,(m)/(s^(2)) )\cdot (0.4\,m)}`

`v = 2.913\,(m)/(s)`

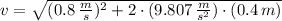
The maximum compression of the spring is calculated by using the Principle of Energy Conservation:

`(3\,kg)\cdot (9.807\,(m)/(s^(2)))\cdot (0.4\,m) + (1)/(2)\cdot (3\,kg)\cdot (2.913\,(m)/(s) )^(2) = (3\,kg) \cdot (9.807\,(m)/(s^(2)))\cdot (0.4\,m-\Delta s) + (1)/(2)\cdot (2000\,(N)/(m))\cdot (\Delta s) ^(2)`

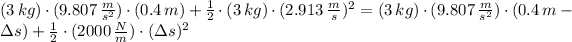
After some algebraic handling, a second-order polynomial is formed:

`12.728\,J = (1)/(2)\cdot (2000\,(N)/(m) )\cdot (\Delta s)^(2) - (3\,kg)\cdot (9.807\,(m)/(s^(2)) )\cdot \Delta s`

`1000\cdot (\Delta s)^(2)-29.421\cdot \Delta s - 12.728 = 0`

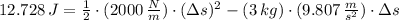
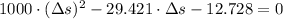
The roots of the polynomial are, respectively:

`\Delta s_(1) \approx 0.128\,m`

`\Delta s_(2) \approx -0.099\,m`

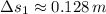
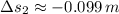
The first root is the only solution that is physically reasonable. Then, the elongation of the spring is:

`\Delta s \approx 0.128\,m`

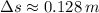
The maximum height that the block reaches after rebound is:

`(3\,kg) \cdot (9.807\,(m)/(s^(2)) )\cdot (0.4\,m-\Delta s) + (1)/(2)\cdot (2000\,(N)/(m))\cdot (\Delta s)^(2) = (3\,kg)\cdot (9.807\,(m)/(s^(2)) )\cdot y_(max)`

`y_(max) = 0.829\,m`