Answer:
(a) Probability that a visually impaired student gets less than 6.5 hours of sleep is 0.1390.
(b) P(6.9 hours < X < 10.6 hours) = 0.6172
(c) Forty percent of students get less than 8.26 hours of sleep on a typical day.
Explanation:
We are given that Researchers found that visually impaired students averaged 8.8 hours of sleep, with a standard deviation of 2.12 hours.
Assume that the number of hours of sleep for these visually impaired students is normally distributed.
Let X = number of hours of sleep for these visually impaired students
So, X ~ Normal(
 )
)
The z-score probability distribution for normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = mean hours of sleep = 8.8 hours
= mean hours of sleep = 8.8 hours
 = standard deviation = 2.12 hours
= standard deviation = 2.12 hours
(a) Probability that a visually impaired student gets less than 6.5 hours of sleep is given by = P(X < 6.5 hours)
P(X < 6.5 hours) = P(
 <
<
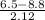 ) = P(Z < -1.085) = 1 - P(Z
) = P(Z < -1.085) = 1 - P(Z
 1.085)
1.085)
= 1 - 0.8610 = 0.1390
The above probability is calculated by looking at the value of x = 1.085 in the z table which will lie in between x = 1.08 and x = 1.09.
(b) Probability that a visually impaired student gets between 6.9 and 10.6 hours of sleep is given by = P(6.9 hours < X < 10.6 hours)
P(6.9 hours < X < 10.6 hours) = P(X < 10.6 hours) - P(X
 6.9 hours)
6.9 hours)
P(X < 10.6 hours) = P(
 <
<
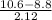 ) = P(Z < 0.85) = 0.80234
) = P(Z < 0.85) = 0.80234
P(X
 6.9 hours) = P(
6.9 hours) = P(


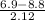 ) = P(Z
) = P(Z
 -0.896) = 1 - P(Z < 0.896)
-0.896) = 1 - P(Z < 0.896)
= 1 - 0.81487 = 0.18513
The above probability is calculated by looking at the value of x = 0.85 and x = 0.896 in the z table which will lie in between x = 0.89 and x = 0.90.
Therefore, P(6.9 hours < X < 10.6 hours) = 0.80234 - 0.18513 = 0.6172
(c) We have to find that Forty percent of students get less than how many hours of sleep on a typical day, that is;
P(X <
 ) = 0.40 {where
) = 0.40 {where
 is the hours of sleep}
is the hours of sleep}
P(
 <
<
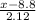 ) = 0.40
) = 0.40
P(Z <
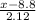 ) = 0.40
) = 0.40
Now, in the z table the critical value of x for which the probability area is less than 40% is -0.2533, that means;
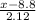 = -0.2533
= -0.2533
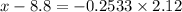
 = 8.8 - 0.536996 = 8.26
= 8.8 - 0.536996 = 8.26
Therefore, Forty percent of students get less than 8.26 hours of sleep on a typical day.