The slope of JK is -6/5.
The slope of PQ is 12/ 15.
These lines are neither parallel nor perpendicular.
Explanation:
From the graph shown,
It can be determined that the point J is (0,5) and K is (10,-7).
The point P is (-5,-8) and Q is (10,4).
The formula for slope is given by,
Slope =
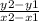
To find the slope of line JK :
J ⇒ (0,5) = (x1,y1)
K ⇒ (10,-7) = (x2,y2)
Slope of JK =

⇒
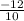
⇒
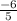
∴ The slope of JK is -6/5.
To find the slope of line PQ :
P ⇒ (-5,-8) = (x1,y1)
Q ⇒ (10,4) = (x2,y2)
Slope of PQ =
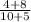
⇒
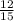
∴ The slope of PQ is 12/ 15.
To find the relation between two lines :
- The parallel lines have same slope.
- The perpendicular lines have a slope of negative reciprocal.
∴ These lines are neither parallel nor perpendicular.