Answer:
The ratio of radius of A to that of B is
 .
.
Step-by-step explanation:
The resistance of a wire is given by :
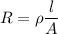
l is length of wire
A is area of cross section
Resistance of wire A is :
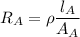 .......(1)
.......(1)
Resistance of wire B,
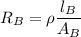 .....(2)
.....(2)
As
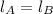 and
and
 (given)
(given)
From equation (1) and (2) and putting given condition, we get :
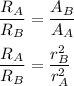
Since,
 . So,
. So,
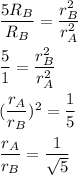
So, the ratio of radius of A to that of B is
 .
.