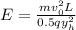Complete Question:
An charge with mass mand charge qis emitted from the origin, (x,y)=(0,0) . A large, flat screen is located at x=L. There is a target on the screen at y positiony_h, where y_{\rm h} /> 0 . In this problem, you will examine two differentways that the charge might hit the target. Ignore gravity in thisproblem.
a.)
Assume that the charge is emitted withvelocity v_0 in the positive x direction. Between the originand the screen, the charge travels through a constant electricfield pointing in the positive y direction. What shouldthe magnitude Eof the electric field be if the charge is to hit the target on thescreen?
Express your answer in terms ofm,q,y_h, v_0, and L.
b.)
Now assume that the charge is emitted withvelocity v_0 in the positive y direction. Between the originand the screen, the charge travels through a constant electricfield pointing in the positive x direction. What shouldthe magnitude E of the electric field be if the charge is to hit the target on thescreen?
Express your answer in terms ofm,q,y_h, v_0, and L.
Answer:
a)

b)
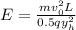
Step-by-step explanation:
The velocity of charge in the x direction = v₀
The time required by the charge to hit the screen at a distance L,
t = L/v₀
The force on the charge, F = qE
F = ma
Equating the two relations for force
ma = qE
acceleration of the charge, a = qE/m
The initial velocity of the charge along the y-direction is o, the vertical distance covered by the charge is:
y = 0.5at²
substituting the relations for a and t
y = 0.5* (qE/m)*(L/v₀)²

If the charge is to hit the target on the screen
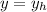
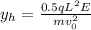
Making E the subject of the formula, the magnitude of the electric field is:

b)
The velocity of charge in the y direction = v₀
The time required by the charge to hit the screen at a height
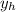 ,
,
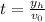
The force on the charge, F = qE
F = ma
Equating the two relations for force
ma = qE
acceleration of the charge, a = qE/m
The initial velocity of the charge along the x-direction is o, the horizontal distance covered by the charge is:
x(t) = 0.5at²
substituting the relations for a and t
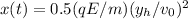

If the charge is to hit the target on the screen
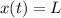
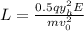
Making E the subject of the formula, the magnitude of the electric field is: