Answer:
Dan is going about 1.30m/s fast as his feet hit the ground.
Step-by-step explanation:
From the conservation of linear momentum, we know that the momentum of the system must be equal before and after Dan jumps. So, we can express this with the equation:
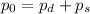
Where
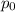 is the momentum of Dan and the skateboard before the jump,
is the momentum of Dan and the skateboard before the jump,
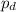 is the momentum of Dan after the jump and
is the momentum of Dan after the jump and
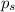 is the momentum of the skateboard after the jump.
is the momentum of the skateboard after the jump.
Now, as momentum is equal to mass times velocity, we can write the equation as:
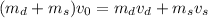
Solving for Dan's final speed
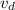 and computing, we get:
and computing, we get:

It means that Dan has a speed of about 1.30m/s when his feet hit the ground.