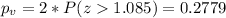Question

In a sample of 60 adults selected randomly from one town, it is found that 12 of them have been exposed to a particular strain of the flu. The test statistic is z=1.08. Find the P-value for a test of the claim that the proportion of all adults in the town that have been exposed to this strain of the flu is different to 15% (H1: p ≠0.15 ).

Answer 1

`z=\frac{0.2 -0.15}{\sqrt{(0.15(1-0.15))/(60)}}=1.085`

`p_v =2*P(z>1.085)=0.2779`

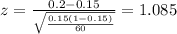
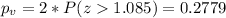
Explanation:

Data given and notation

n=60 represent the random sample taken

X=12 represent the adults exposed to a particular strain of the flu

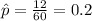`\hat p=(12)/(60)=0.2` estimated proportion of adults exposed to a particular strain of the flu

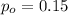`p_o=0.15` is the value that we want to test

`\alpha` represent the significance level

z would represent the statistic (variable of interest)

`p_v` represent the p value (variable of interest)

Concepts and formulas to use

We need to conduct a hypothesis in order to test the claim that the true proportion is 0.15 or no.:

Null hypothesis:
`p=0.15`

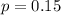
Alternative hypothesis:
`p \\eq 0.15`

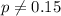
When we conduct a proportion test we need to use the z statistic, and the is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

The One-Sample Proportion Test is used to assess whether a population proportion
`\hat p` is significantly different from a hypothesized value
`p_o`.

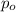Calculate the statistic

Since we have all the info requires we can replace in formula (1) like this:

`z=\frac{0.2 -0.15}{\sqrt{(0.15(1-0.15))/(60)}}=1.085`

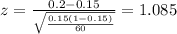
Statistical decision

It's important to refresh the p value method or p value approach . "This method is about determining "likely" or "unlikely" by determining the probability assuming the null hypothesis were true of observing a more extreme test statistic in the direction of the alternative hypothesis than the one observed". Or in other words is just a method to have an statistical decision to fail to reject or reject the null hypothesis.

The next step would be calculate the p value for this test.

Since is a bilateral test the p value would be:

`p_v =2*P(z>1.085)=0.2779`