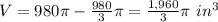Question

12. The cylinder to the left contains two congruent hollow cones. If the

cylinder's height is 20 inches and its diameter is 14 inches, find the
volume of the solid.

Answer 1

The volume of the solid is

`V=(1,960)/(3) \pi\ in^3`

Explanation:

step 1

Find the volume of the cylinder

The volume of the cylinder is given by the formula

`V=\pi r^(2) h`

we have

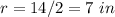`r=14/2=7\ in` ---> the radius is half the diameter

`h=20\ in`

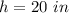
substitute the values

`V=\pi (7)^(2) (20)=980\pi\ in^3`

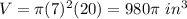
step 2

Find the volume of the two congruent hollow cones

The volume of the two cones is given by the formula

`V=2[(1)/(3) \pi r^(2)h]`

we have

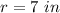`r=7\ in` ---> is the same that the radius of cylinder

`h=10\ in` ----> is half that the height of cylinder

substitute

`V=2[(1)/(3) \pi (7)^(2)(10)]`

`V=(980)/(3) \pi\ in^3`

step 3

To find out the volume of the solid subtract the volume of the two cones from the volume of the cylinder

`V=980\pi-(980)/(3) \pi=(1,960)/(3) \pi\ in^3`