Answer:
y=-x²+3x+5.
Explanation:
1) the common view of the quadratic function is y=ax²+bx+c, where a, b and c - numbers;
2) according to the equation above, it needed to substitute the given coordinates and to make up the system of the equations:
point (0;5): c=5;
poit(1;7): a+b+5=7 ('c' is already known, 5);
point(-2;-5): 4a-2b+5=-5 (c=5);
3) to solve the system:
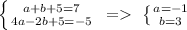
4) finally, if a=-1, b=3 and c=5, then
y=-x²+3x+5.