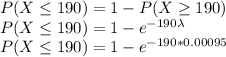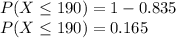Answer:
a)
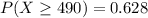
b)
Explanation:
a) This is an exponential distribution question since it is a poisson type problem
Mean rate is 0.95 per 1000 passengers
Mean rate,
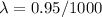
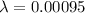 per passenger
per passenger
Probability that at least 490 passengers will have their baggage handled properly before the next mishandling occurs :
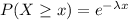
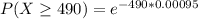
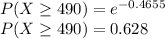
b) Probability that the number will be fewer than 200 passengers