Answer: The pH at equivalence for the given solution is 8.37.
Step-by-step explanation:
We know that,
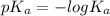
3.46 =

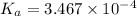
Now, we will calculate the volume of NaOH required to reach the equivalence point as follows.
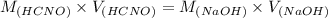
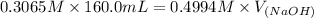
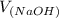 = 98.1978 mL
= 98.1978 mL
The given data is as follows.
M(HCNO) = 0.3065 M
V(HCNO) = 160 mL
M(NaOH) = 0.4994 M
V(NaOH) = 98.1978 mL
So, moles of HCNO will be calculated as follows.
mol(HCNO) =
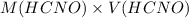
mol(HCNO) =
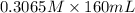
= 49.04 mmol
Now, the moles of NAOh will be calculated as follows.
mol(NaOH) =

mol(NaOH) =
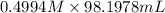
= 49.04 mmol
This means that, 49.04 mmol of both HCNO and NaOH will react to form
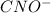 and
and
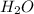 .
.
Here,
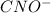 is strong base . So,
is strong base . So,
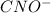 formed = 49.04 mmol
formed = 49.04 mmol
Total volume of the solution is as follows.
Volume of Solution = 160 + 98.1978 = 258.1978 mL
And,
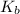 of
of
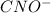 =
=

=

=

The concentration of
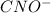 is as follows.
is as follows.
c =
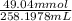
= 0.1899M
Also,
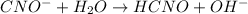
Initial: 0.1899 0 0
Equilibm:0.1899 - x x x
![K_(b) = ([HCNO][OH^(-)])/([CNO^(-)])](https://img.qammunity.org/2021/formulas/chemistry/college/gsrxvzx8gx2mwkg63pxsx67il8xiiipb6q.png)
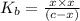
We assume that x can be ignored as compared to c . Hence, above formula can be rewritten as follows.

so, x =
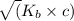
x =
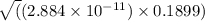
=
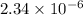
Here, c is much greater than x, this means that our assumption is correct .
so, x =
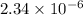 M
M
![[OH^(-)] = x = 2.34 * 10^(-6)](https://img.qammunity.org/2021/formulas/chemistry/college/lmdgi3vtj70znk74u0gstm5j0jp735ylg0.png) M
M
As,
pOH =
![-log [OH^(-)]](https://img.qammunity.org/2021/formulas/chemistry/college/zv1af3ysn0xxbuqqoy4ytmwom7cppopfmk.png)
=
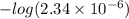
= 5.6307
Also, pH = 14 - pOH
= 14 - 5.6307
= 8.3693
or, = 8.37 (approx)
Thus, we can conclude that the pH at equivalence for the given solution is 8.37.