Question

1. A coin-operated drink machine was designed to discharge a mean of 7 ounces of coffee per cup. In a test of the machine, the discharge amounts in 13 randomly chosen cups of coffee from the machine were recorded. The sample mean and the sample standard deviation were 7.08 ounces and 0.22 ounces, respectively. If we assume that the true amounts are normally distributed, is there enough evidence, at the 0.1 level of significance, to conclude that the true mean discharge, µ, differs from 7 ounces? Carry your intermediate computations to at least three decimal places.

Answer 1

No, at the 0.1 level of significance, there is not enough evidence to conclude that the true mean discharge, µ, differs from 7 ounces.

Explanation:

We are given that a coin-operated drink machine was designed to discharge a mean of 7 ounces of coffee per cup. In a test of the machine, the discharge amounts in 13 randomly chosen cups of coffee from the machine were recorded.

The sample mean and the sample standard deviation were 7.08 ounces and 0.22 ounces, respectively.

Let
`\mu` = true mean discharge amount

SO, Null Hypothesis,
`H_0` :
`\mu` = 7 ounces {means that the true mean discharge, µ, does not differs from 7 ounces}

Alternate Hypothesis,
`H_a` :
`\mu \\eq` 7 ounces {means that the true mean discharge, µ, differs from 7 ounces}

The test statistics that will be used here is One-sample t test statistics because we don't know about the population standard deviation;

T.S. =
`\frac{\bar X -\mu}{{(s)/(√(n) ) } }` ~
`t_n_-_1`

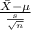where,
`\bar X` = sample mean discharge amount = 7.08 ounces

s = sample standard deviation = 0.22 ounces

n = sample of coffee cups = 13

So, test statistics =
`\frac{7.08-7 }{{(0.22)/(√(13) ) } }` ~
`t_1_2`

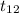
= 1.311

Now at 0.1 significance level, the t table gives critical values between -1.782 and 1.782 at 12 degree of freedom for two-tailed test. Since our test statistics lies within the range of critical values of t so we insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the the true mean discharge, µ, does not differs from 7 ounces.