Answer: Dimensions should be 510 feet to maximize the total area of the two fields.
Explanation:
Since we have given that
Perimeter of field = 2040 feet
Let the width of rectangle be 'x'
Let the length of rectangle be '2x'
So, According to question, it becomes,
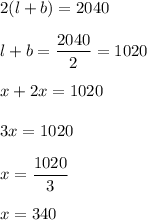
So, the length would be
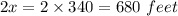
If another field is square,
So, the dimensions would be
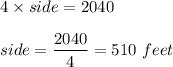
Now, Area of rectangle would be
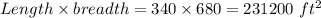
Area of square would be
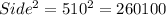 sq. ft
sq. ft
So, Dimensions should be 510 feet to maximize the total area of the two fields.