Question

A car insurance company suspects that the younger the driver is, the more reckless a driver he/she is. They take a survey and group their respondents based on age. Of 217 respondents between the ages of 16-25 (Group 1), 183 claimed to wear a seat belt at all times. Of 398 respondents who were 26+ years old (Group 2), 322 claimed to wear a seat belt at all times. Find a 95% confidence interval for the difference in proportions. Can it be concluded that there is a difference in the proportion of drivers who wear a seat belt at all times based on age group?

Answer 1

The confidence interval for the difference in proportions is

`-0.028\leq p_1-p_2 \leq 0.096`

No. As the 95% CI include both negative and positive values, no proportion is significantly different from the other to conclude there is a difference between them.

Explanation:

We have to construct a confidence interval for the difference of proportions.

The difference in the sample proportions is:

`p_1-p_2=x_1/n_1-x_2/n_2=(183/217)-(322/398)=0.843-0.809\\\\p_1-p_2=0.034`

The estimated standard error is:

`\sigma_(p_1-p_2)=\sqrt{(p_1(1-p_1))/(n_1)+(p_2(1-p_2))/(n_2) } \\\\\sigma_(p_1-p_2)=\sqrt{(0.843*0.157)/(217)+(0.809*0.191)/(398) } \\\\\sigma_(p_1-p_2)=√(0.000609912+0.000388239)=√(0.000998151) \\\\ \sigma_(p_1-p_2)=0.0316`

The z-value for a 95% confidence interval is z=1.96.

Then, the lower and upper bounds are:

`LL=(p_1-p_2)-z*\sigma_p=0.034-1.96*0.0316=0.034-0.062=-0.028\\\\\\UL=(p_1-p_2)+z*\sigma_p=0.034+1.96*0.0316=0.034+0.062=0.096`

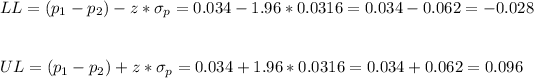
The confidence interval for the difference in proportions is

`-0.028\leq p_1-p_2 \leq 0.096`

Can it be concluded that there is a difference in the proportion of drivers who wear a seat belt at all times based on age group?

No. It can not be concluded that there is a difference in the proportion of drivers who wear a seat belt at all times based on age group, as the confidence interval include both positive and negative values.

This means that we are not confident that the actual difference of proportions is positive or negative. No proportion is significantly different from the other to conclude there is a difference.