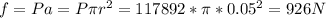Answer:
926 N
Step-by-step explanation:
Metric unit conversion:
R = 18 cm = 0.18 m
r = 5 cm = 0.05 m
The pressure exerted by the F = 12000N car on the wider arm would be ratio of the gravity over area
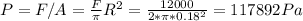
The pressure must be the same on the smaller pressure for it to be able to start lifting the car. We can calculate the force f acting on it: