Question

A data set includes data from student evaluations of courses. The summary statistics are nequals89​, x overbarequals3.58​, sequals0.53. Use a 0.01 significance level to test the claim that the population of student course evaluations has a mean equal to 3.75. Assume that a simple random sample has been selected. Identify the null and alternative​ hypotheses, test​ statistic, P-value, and state the final conclusion that addresses the original claim.

Answer 1

|t| =| - 3.0303| = 3.03

Hence we rejected null hypothesis.

The claim that the population of student course evaluations has a mean is not equal to 3.75

Explanation:

Step(i)

A data set includes data from student evaluations of courses.

Given n= 89

sample mean x⁻ = 3.58

Sample Standard deviation (S) = 0.53

Given data population of student course evaluations has a mean equal to 3.75.

μ = 3.75

Step(ii)

Null hypothesis:-H₀: the population of student course evaluations has a mean equal to 3.75

μ = 3.75

Alternate hypothesis :- H₁: μ ≠ 3.75

Level of significance :-∝=0.01

The test statistic

`t = (x^(-) -mean)/((S)/(√(n) ) )`

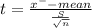
Step(iii):

The degrees of freedom γ=n-1 = 89-1=88

tabulated value t = 2.3733

Calculated value

`t = (3.58-3.75)/((0.53)/(√(89) ) )`

t = - 3.0303

|t| =| - 3.0303| = 3.03

The tabulated value of 't' for 88 degree of freedom at 1% of level of significance is 2.3733

since calculated value t=3.03 is greater than tabulated value t = 2.3733 of t

Hence we rejected null hypothesis.

the claim that the population of student course evaluations has a mean is not equal to 3.75